CTF Writeup: Playagame (OTW Advent 2018)
Problem
Playagame - Net (150)
Global Thermonuclear War, Cleanup Edition
Solves: 28
Service: telnet 18.205.93.120 1203
Author: StevenWhen we connect we are presented with the following screen:
GREETINGS PROFESSOR FALKEN.
SHALL WE PLAY A GAME?
TIC-TAC-TOE
BLACK JACK
GIN RUMMY
HEARTS
BRIDGE
CHECKERS
CHESS
POKER
FIGHTER COMBAT
GUERRILLA ENGAGEMENT
DESERT WARFARE
AIR-TO-GROUND ACTIONS
THEATERWIDE TACTICAL WARFARE
THEATERWIDE BIOTOXIC AND CHEMICAL WARFARE
GLOBAL THERMONUCLEAR WAR, CLEANUP EDITIONAnswering “GLOBAL THERMONUCLEAR WAR, CLEANUP EDITION” takes us to the following screen:
In 2025, the world has been devastated by a nuclear attack and is a nuclear
wasteland. Luckily, the Chinese government has foreseen this disaster and
launched a satellite in orbit that is able to counter the nuclear waste.
Research has shown that nuclear waste is primarily composed of inverted tachyon
and positive lepton radiation, which cancel each other out.
The Chinese satellite uses inverted tachyons (-) and positive leptons (+) that
can each be fired in 9 different patterns over an area of 3 by 3 kilometers.
Your job is to clean up the nuclear waste by positioning the satellite,
selecting a firing mode (- or +) and a firing pattern (1 through 9), and then
firing. The result will be instantaneous, the remaining contaminants per
square kilometer will be indicated on the screen.
Please note that firing the satellite costs money, which the post-apocalyptic
world is in short supply of: don't waste money! Good luck!
Keys:
arrow keys: position satellite
s or c: select firing mode and pattern
f: fire satellite
q: quit and let the world go to waste
Press enter to continue.Okay, so we need to cleanup after a nuclear attack? Nice. Let’s press enter.
We are now presented with a screen like this:
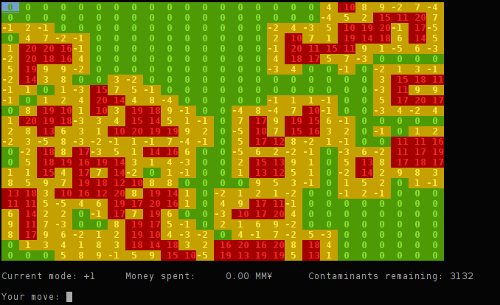
Solution
Moving around on the board and trying out the different firing modes we conclude that:
- all modes affect the 3x3 square centered at the cursor
- all modes are deterministic
- the positive (+) and negative (-) version of the modes cancel
The patterns are as follows:
# 1 # 2 # 3
5 0 -5 1 0 -5 -1 1 2
-1 1 -2 -2 3 -1 1 -1 1
-1 -2 -2 1 0 -1 -1 -1 0
# 4 # 5 # 6
1 0 -1 -3 0 3 -4 0 5
0 -1 0 1 -1 2 2 -1 2
-1 -1 -1 1 1 1 1 2 2
# 7 # 8 # 9
2 1 -2 -2 -1 2 2 0 -2
0 0 -1 0 0 1 -1 0 -1
-1 -2 -1 0 2 1 0 -1 -1These are linearly independent as vectors in R³ˣ³ which means that
they form a basis in R³ˣ³. We can now transform any square S into
any target square T by solving for x in
Ax = T - Sand adding the result to the square S
S + Ax = S + T - S = Twhere A is the matrix containing the coordinates of the patterns in the standard basis on R³ˣ³
To make things easier we express the patterns as vectors in R⁹ instead. Then A is the matrix:
5 1 -1 1 -3 -4 2 -2 2
0 0 1 0 0 0 1 -1 0
-5 -5 2 -1 3 5 -2 2 -2
-1 -2 1 0 1 2 0 0 -1
1 3 -1 -1 -1 -1 0 0 0
-2 -1 1 0 2 2 -1 1 -1
-1 1 -1 -1 1 1 -1 0 0
-2 0 -1 -1 1 2 -2 2 -1
-2 -1 0 -1 1 2 -1 1 -1Finally, solving the problem means that we solve Ax = -S for all 3x3
squares on the board and translate the result x into commands to
send to the server.
Example Run
Code
import numpy as np
import re
patterns = [
# 1
np.array([[ 5, 0, -5],
[-1, 1, -2],
[-1, -2, -2]]),
# 2
np.array([[ 1, 0, -5],
[-2, 3, -1],
[ 1, 0, -1]]),
# 3
np.array([[-1, 1, 2],
[ 1, -1, 1],
[-1, -1, 0]]),
# 4
np.array([[ 1, 0, -1],
[ 0, -1, 0],
[-1, -1, -1]]),
# 5
np.array([[-3, 0, 3],
[ 1, -1, 2],
[ 1, 1, 1]]),
# 6
np.array([[-4, 0, 5],
[ 2, -1, 2],
[ 1, 2, 2]]),
# 7
np.array([[ 2, 1, -2],
[ 0, 0, -1],
[-1, -2, -1]]),
# 8
np.array([[-2, -1, 2],
[ 0, 0, 1],
[ 0, 2, 1]]),
# 9
np.array([[ 2, 0, -2],
[-1, 0, -1],
[ 0, -1, -1]])
]
bad = re.compile(r'(\d)-(\d)')
def parse_board(x):
return np.array([
[int(cell) for cell in row.split(' ') if cell]
for row in bad.sub(r'\1 -\2', x).split('\n') if row
], dtype='int')
def print_board(board):
print('\n'.join(
' '.join(
f'{board[ri, ci]:>3}'
for ci in range(25)
)
for ri in range(25)
))
def solve(board):
solution = []
board = board.copy()
A = np.array(patterns).reshape(9, 9).T
# Solve top left
ci = 1
ri = 1
solution.extend(solve_block(A, board, ri, ci))
board[ri-1:ri+2,ci-1:ci+2] = np.zeros((3,3))
# Solve first column
ci = 1
for ri in range(2, 25, 3):
solution.extend(solve_block(A, board, ri, ci))
board[ri-1:ri+2,ci-1:ci+2] = np.zeros((3,3))
# Solve first row
ri = 1
for ci in range(2, 25, 3):
solution.extend(solve_block(A, board, ri, ci))
board[ri-1:ri+2,ci-1:ci+2] = np.zeros((3,3))
# Solve the rest
for ri in range(2, 25, 3):
for ci in range(2, 25, 3):
solution.extend(solve_block(A, board, ri, ci))
board[ri-1:ri+2,ci-1:ci+2] = np.zeros((3,3))
return (solution, board)
def solve_block(A, board, ri, ci):
block = board[ri-1:ri+2,ci-1:ci+2].reshape(9)
answer = np.linalg.solve(A, -block)
yield from (
(pi+1, int(round(c)), ri, ci)
for pi, c in enumerate(answer)
if int(round(c)) != 0
)
def verify(solution, board):
board = board.copy()
for pi, c, ri, ci in solution:
board[ri-1:ci+2,ri-1:ci+2] += c*patterns[pi-1]
return board
def select(p, positive=True):
yield 's'
if positive:
yield '+'
else:
yield '-'
yield str(p)
def apply_solution(solution):
solution.sort(key=lambda t: (t[2], t[3]))
posx = 0
posy = 0
for p, c, ri, ci in solution:
x = ci
y = ri
diffx = posx - x
if diffx > 0:
yield from ('l'*diffx)
elif diffx == 0:
pass
else:
yield from ('r'*(-diffx))
posx = x
diffy = posy - y
if diffy > 0:
yield from ('u'*diffy)
elif diffy == 0:
pass
else:
yield from ('d'*(-diffy))
posy = y
if c == 0:
pass
else:
yield from select(p, c > 0)
yield from ('f'*abs(c))
if __name__ == '__main__':
import string
import sys
import telnetlib
if sys.argv[1:2] == 'telnet':
# Thanks SO!
ansi_escape = re.compile(rb'\x1B\[[0-?]*[ -/]*[@-~]')
# Should theoretically work, but takes ages to run for some reason
with telnetlib.Telnet("18.205.93.120", 1203) as tn:
tn.write(b"GLOBAL THERMONUCLEAR WAR, CLEANUP EDITION\n")
tn.write(b"\n")
tn.read_until(b"Press enter to continue")
print("Game Start!")
tn.read_until(b"\x30\x48\n")
valid = set(string.printable.encode('ascii'))
lines = []
for i in range(25):
line = tn.read_until(b"\x0d\x0a")
lines.append(ansi_escape.sub(b'', line).decode('ascii').strip())
print(lines[-1])
tn.read_until(b'\n')
board = parse_board('\n'.join(lines))
print("Parsed board:")
print_board(board)
solution = solve(board)
print("Sending solution...")
tn.write(''.join(apply_solution(solution)).encode('ascii'))
tn.read_until(b"#########")
tn.interact()
else:
print("Paste board here, finish with ^D", file=sys.stderr)
board = parse_board(sys.stdin.read())
solution, solved = solve(board)
print(''.join(apply_solution(solution)))